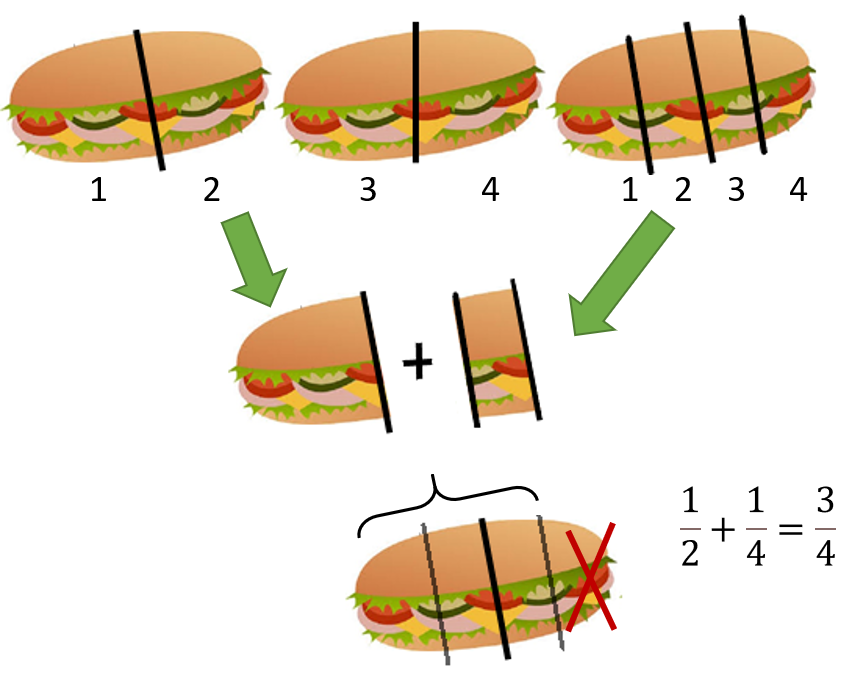
The Different Meanings of Fraction

Over the last month, I have been working with the amazing master teachers at the Columbus Regional Math Collaborative, putting together a fun filled summer camp to help boost children’s knowledge of fractions before they enter middle school. Of course, if I want to boost their knowledge of the meaning of fractions, I knew I needed to reread some of my favorite research articles and books! What a great time to add to Half-a-Blog!
At the camp, we plan to start with the meaning of fractions before launching into fraction division – my favorite operation – and focusing on how these clever numbers are affected by operations. Hence, we named the camp….
Operation Super Solvers!
I’m so excited about the cool activities we are planning for the camp. We have to be pretty sneaky to make everything fun while also tackling the challenging topic of fractions. As usual, the background research is very interesting and a little daunting when it comes to the many ways children conceptualize fractions.
What are ways that children think about fractions?
Most of the time when we introduce fractions, we think of partitioning a whole. Believe it or not, the part-whole relationship is just one of the five ways children need to think about fractions, according to most researchers (see Charalambous & Pitta-Pantazi, 2007 or Tien & Siegler, 2018). That’s just one 1 out of 5 concepts that children need to master. And the part-whole relationship is more complicated than you would think!
Consider these two drawings:
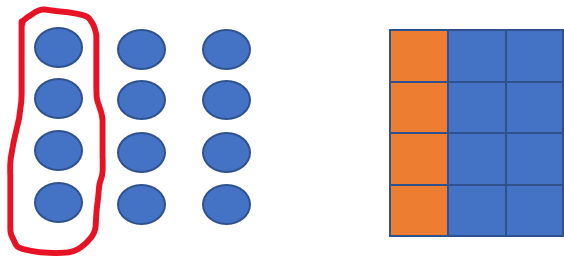
In one, you have one whole area partitioned into equal parts. In the other you have a collection of objects divided into equal groups. Think about what children need to master to fully understand what the numerator and denominator mean.
- What is the whole we are talking about?
- How are we sure that the whole is divided equally?
- What are the total number of parts?
- What are the number of parts represented by the fraction?
- Will the part-whole relationship stay the same if I move the parts around?

Most of the time, the part-whole relationship is only discussed for fractions less than one. Can you reimage the drawings above if the fraction was 15 twelfths?
The Part-Whole Concept is one the Beginning!
Some researchers have constructed a hierarchical chart to show the relationship between the different ways children think about fractions (Charalambous & Pitta-Pantazi, 2007; Behr et al.,1983; ). I’m actually designing a research project this summer loosely based upon this – especially since I’m not entirely sure I buy into this diagram. But, it’s a good visual aid!
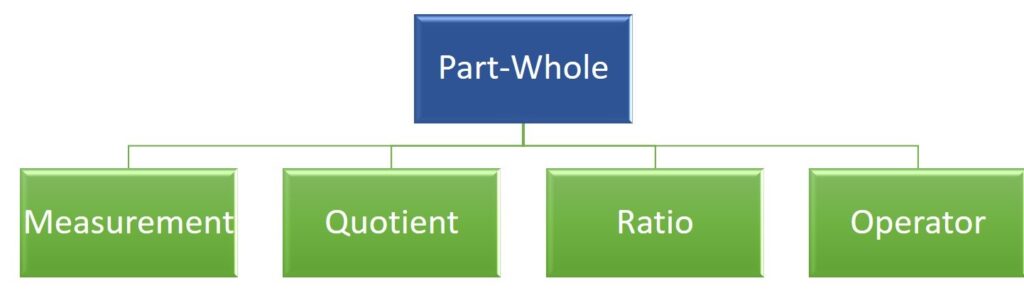
While some countries limit the concepts of fraction to partitioning and quantifying, several research studies that analyze how children discover fraction concepts rely on four constructs: measure, quotient, ratio/rate and operator. Teachers can use different tasks or questions to help children develop a deeper understanding of fractions.
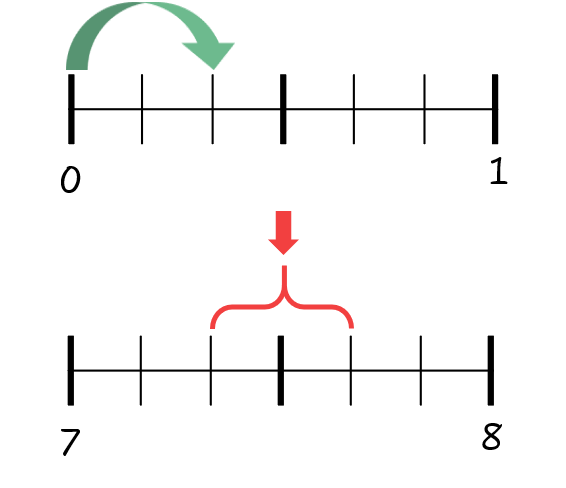
Measure (or Magnitude)
Within this concept, we want children to see a fraction as a number. Teachers can set up tasks that require children to find a fraction on a number line and to connect that a fraction can represent a distance from zero. But, it’s also important that children understand that a distance between two numbers can also be a fraction. Placing fractions on clothes lines is a rich activity, and there are many strategies to explore when comparing fractions to benchmarks (e.g. ½, 1, etc.). For example, which fraction is larger, 7/8 or 10/11? A quick way to decide is to compare the distance each fraction is from 1. The first is 1/8 from one. The second is only 1/11.
Quotient
How many times have we heard, “A fraction is just a little division problem?” We say three-fourths is three divided by four, but we don’t think it is a quotient (the result of division) as easily. When I ask my pre-service teachers, “Show me how you could share 3 sub sandwiches with 4 people?” they typically begin dividing two subs in half and the last sub into fourths. Understanding that ¾ is a more direct answer takes time. “What if you divide 8 sandwiches among 7 people?” That typically leads to a mixed number before an improper fraction becomes apparent.
Ratio/Rate
While we usually don’t dive into ratios and rates until middle school, both of these concepts are pervasive! Four out of five rotten tomatoes? Costs per person? Miles per gallon? As one of the master teachers aptly observed – we use the word “per” without really introducing it as a rate. A famous task that brings out this concept is the “Orange Juice Task” posed by Gerald Noelting (1980) in which children were making orange juice for a party by combining glasses of concentrated orange juice and water. One child combined 3 glasses of orange juice with 5 glasses of water, but another combined 5 glasses of orange juice with 8 glasses of water. Which pitcher would taste more orange?
Operator
This concept is simple when you think of three-fourths as three quarters or three one-fourths. However, the concept can also be more complex when you begin to think of a fraction as a composition of operations or dare I say a function that transforms one number into another. When we think, “I need to take ¾ of the recipe” we reduce or shrink the amount of the recipe.

Fractions are Cool Numbers
Here I go again on the nerd train, but fractions are cool numbers! They open up the door for children to think about an entirely new number system! And I haven’t even started to talk about decimal fractions, rational numbers, and how there are infinitely many of them between each fraction!!
As I proofread this post, I found it fascinating to see the interplay of number concepts with operation concepts. It made me wonder, when do we cross the line between thinking about a set of numbers, such as fractions, and thinking about operations, such as division? I think there are some interesting research questions to study this summer, along with teaching all about fractions at the camp!
References & Research Articles
Behr, M. J., Lesh, R., Post, T., & Silver, E. A. (1983). Rational number concepts. Acquisition of Mathematics Concepts and Processes, 91, 126.
Charalambous, C., & Pitta-Pantazi, D. (2007). Drawing on a Theoretical Model to Study Students’ Understandings of Fractions. Educational Studies in Mathematics, 64(3), 293-316. https://doi.org/10.1007/s10649-006-9036-2
Noelting, G. (1980). The Development of Proportional Reasoning and the Ratio Concept Part I – Differentiation of Stages. Educational Studies in Mathematics, 11(2), 217-253.
Schumacher, R. F., Jayanthi, M., Gersten, R., Dimino, J., Spallone, S., & Haymond, K. S. (2018). Using the Number Line to Promote Understanding of Fractions for Struggling Fifth Graders: A Formative Pilot Study. Learning Disabilities Research & Practice (Wiley-Blackwell), 33(4), 192-206. https://doi.org/10.1111/ldrp.12169
Tian, J., & Siegler, R. S. (2018). Which Type of Rational Numbers Should Students Learn First? Educational Psychology Review, 30(2), 351-372. https://doi.org/10.1007/s10648-017-9417-3