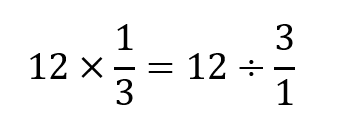Launching Big Ideas about Fractions

A teacher who loves the comic book series, The Mysterious I.D. Vide and Newton’s Nemesis, recently asked me “How would should I use it?” Up until now, I’ve been hesitant to prescribe a “best practice” because I believe every classroom and every teacher, just like every child, has different needs and unique perspectives that drive mathematical learning. In truth, I wrote the series as a fun way to launch great classroom conversations about the big ideas that are foundational to understanding fraction multiplication and division. So, the question is, “What are those big ideas?”
Throughout the series, my goal was to sprinkle clues and dialogues about math concepts that would make children wonder, “Is that true?” or “Will that always work?”, with the idea that it would inspire classroom conversations. By the end of the first comic book in the series, I wanted children to explore and be able to explain not only why multiplying by ½ is the same as dividing by 2, but also be able to connect it to a math equation such as 12 x ½ = 12 ÷ 2, or even extend it to:
It is true that both equations are, obviously, equivalent. However, three over one has some subtle challenges for most children who mistakenly believe that all fractions are less than one! Experienced teachers are smiling right now as they recall students asking, “Where did that 1 come from???” As I learned on my first day student teaching, the most subtle things can cause bewildering confusion among students!
In the first issue of Newton’s Nemesis, Theo explains to his little sister that dividing by 3 is the same as taking a third of something, but there are some big ideas that need exploration in order for children to make sense out of our equation. For example, when you take 1/3 of 12, why is it symbolically 12 x 1/3? Or is it 1/3 x 12?

To truly understand the relationship between division by whole numbers and multiplication by unit fractions, we need to ask big questions in our classrooms:
- What does multiplying by a whole number mean?
- What does multiplying by a unit fraction mean?
- Why is multiplying by a unit fraction the same as dividing by its denominator?
After reading the first issue of the comic book series, I would ask the class a sequence of questions, allowing them to justify their answers with fraction rods or by drawing models. For example:
-
-
- Theo explained to his little sister that dividing by 3 is the same as taking a third of something. Do you agree? Why?
- What if she divided by 5? Or 7? Is there a pattern? If so, can you explain what it is?
-
By the second question, students should be using their understanding of a fraction, 1/b, as a whole divided into b parts, to justify their claim that taking 1/b is the same as dividing by b. After the class has come to consensus in words, it’s time to record our findings using mathematical notation.
The next question for the class: When Leah said, “12 divided by 3 is 4”, I can write the math sentence “12 ÷ 3 = 4.” How can I write, “4 is 1/3 of 12” as a math sentence?
That is a challenging question. Children will begin to guess! “Is it ‘4 = 1/3 ÷ 12?’” or “How about ‘4 = 1/3 minus 12?’” and one might even guess correctly! The point is not to guess the answer but explore what each operation means to discover the answer. What does it mean to divide by 12? Subtract 12? Multiply 12?
Be careful not to dive too quickly into what dividing by 1/3 means, since the goal is to explore what fraction multiplication means. As students form groups to determine the answer to our question, “How can we write, ‘4 is 1/3 of 12’ as a math sentence?”, they might struggle because this is a big question. You can always encourage them as Theo’s mother did, “Making mistakes means you’re learning.”
Struggling students can also be prompted to work with whole number questions to recall their operations. For example, “Can you use rods or drawings to show what 12 divided by 3 is? Or what 3 times 4 is?” Before long, someone usually will begin to write “1/3” twelve times and discover the sum of 12 thirds is indeed 4. And then you know you are almost done!
Even if their solution equals 4, we have not yet explored the true meaning of 1/3 x 12. Using our A x B definition, it means 1/3 group of 12! That’s the final big idea we needed! Because we now know all of these are the same:
Recall that A x B means A groups of B, as defined by the Common Core. Therefore, if you sum twelve 1/3’s that is 12 groups of 1/3.
1/3 of 12
1/3 group of 12
1/3 x 12
12 x 1/3
12 ÷ 3
Now, if you want to extend it to the more subtly challenging question:
We might need to do a little rapping!